Desenlerde Sonsuzluğu Bulmanıza Olanak Sağlayan Olay: Hilbert Eğrisi
Hilbert Eğrisi: Fraktal Geometriye Bir Bakış
Hilbert Eğrisi, matematikteki fraktal geometriye ait ilginç bir örnek olarak karşımıza çıkar. Alman matematikçi David Hilbert tarafından 20. yüzyılın başlarında tanıtılan bu eğri, matematiksel bir desen ve yapıya sahiptir. Hilbert Eğrisi’nin oluşum süreci, basit bir şekilden başlayarak karmaşık bir fraktal desenin ortaya çıkmasını sağlar.
Hilbert Eğrisi’nin oluşturulması, başlangıçta bir kenarı birim uzunluğunda olan bir kare ile başlar. Bu kare, dört eşit parçaya bölünür ve bu parçalar birbirine bağlanarak bir yol oluşturur. Ardından, her bir kare parçası, kendi içinde benzer bir yapıya sahip olan daha küçük karelerle doldurulur. Bu işlem, her seviyede daha fazla kare ve bağlantı ekleyerek devam eder. Sonuç olarak, her seviyede daha karmaşık ve ayrıntılı bir eğri ortaya çıkar.
Hilbert Eğrisi’nin ilginç özelliklerinden biri, özbenzerlik özelliğine sahip olmasıdır. Özbenzerlik, eğrinin daha küçük ölçekteki her bölümünün, daha büyük ölçekteki tüm eğriyi yansıtması anlamına gelir. Yani, Hilbert Eğrisi’nin herhangi bir parçası, tüm eğrinin aynasıdır. Bu özbenzerlik özelliği, eğrinin sonsuz bir detay ve tekrarlamalarla dolu olduğunu gösterir.
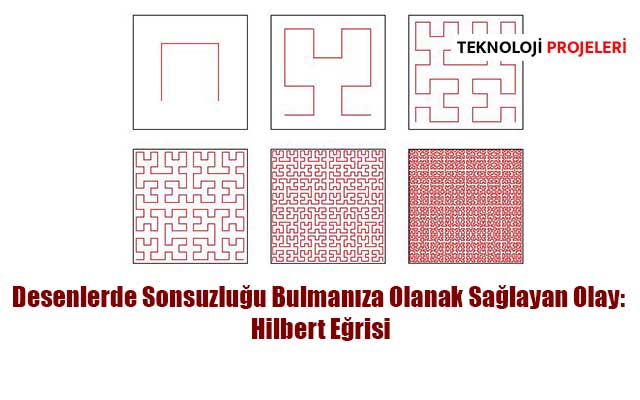
Hilbert Eğrisi’nin matematiksel açıdan incelenmesi, fraktal geometri, topoloji ve kesirli boyutlar gibi konuları içerir. Fraktal geometri, doğada bulunan karmaşık desenlerin matematiksel temsilini inceler. Hilbert Eğrisi, bu alanda yapılan araştırmaların önemli bir örneğidir ve fraktal geometri teorilerine katkıda bulunmuştur.
Hilbert Eğrisi’nin tarihsel gelişimi, matematikçi David Hilbert’in çalışmalarıyla ilişkilidir. Hilbert, 19. yüzyılda Fransız matematikçi Pierre-François Verhulst’un yaptığı özbenzerlik çalışmalarını takip etmiştir. Hilbert, kendi çalışmalarında bu özbenzerlik fikrini genişletmiş ve Hilbert Eğrisi’ni tanıtmıştır.
Hilbert Eğrisi’nin pratik uygulamaları da bulunmaktadır. Bilgisayar grafikleri ve veri sıkıştırma gibi alanlarda, Hilbert Eğrisi’nin özbenzerlik ve tekrarlanabilirlik özellikleri kullanılarak verilerin etkin bir şekilde temsil edilmesi sağlanabilir. Ayrıca, Hilbert Eğrisi, karmaşık sistemlerin analizinde ve modellemesinde de kullanılmaktadır.
Sonuç olarak, Hilbert Eğrisi, matematikte fraktal geometriye ait ilginç bir örnektir. Basit bir başlangıçtan karmaşık bir desen oluşturarak özbenzerlik ve tekrarlanabilirlik özellikleri gösterir. Matematikçi David Hilbert’in çalışmalarıyla ortaya çıkan bu eğri, matematiksel araştırmalarda, uygulamalarda ve öğrenmede önemli bir rol oynamaktadır.
Önerilen Yazı: Matematikte Bilinmeyene Neden X İfadesi Kullanılır?



