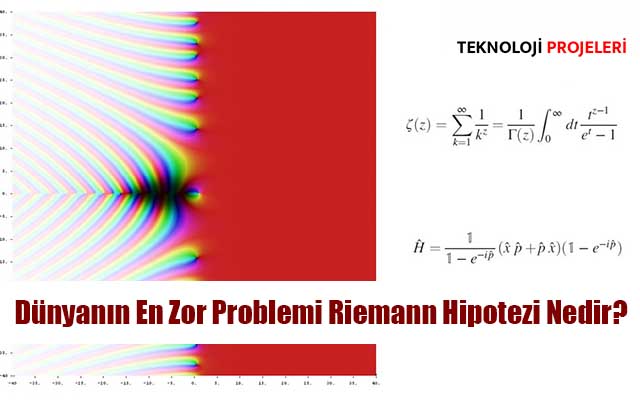
Dünyanın En Zor Problemi Riemann Hipotezi Nedir?
Riemann Hipotezi Nedir?
Riemann Hipotezi, matematiğin en önemli açık problemlerinden biridir. Bu hipotez, asal sayıların dağılımı hakkındaki bir teoriyi ortaya koyar ve matematikçilerin, asal sayıların davranışlarını anlamak için yüzyıllardır çalıştığı bir konudur. Riemann Hipotezi, hem matematiksel teorilerin geliştirilmesi hem de kriptografi gibi birçok alanda kullanılmaktadır. Bu yazıda, Riemann Hipotezi hakkında daha detaylı bilgi vereceğiz.
Riemann Hipotezi, 19. yüzyılda yaşamış olan Alman matematikçi Bernhard Riemann tarafından ortaya atılmıştır. Bu hipotez, asal sayıların dağılımı hakkındaki bir teoriyi ifade eder. Riemann, bu teoriyi geliştirirken, asal sayıların sayısı hakkındaki bir formül önerdi. Bu formül, sadece bir hipotez olarak kalmıştır ve henüz kanıtlanmamıştır.
Riemann Hipotezi, asal sayıların dağılımı hakkındaki bir teoriyi ifade ettiği için, matematikçilerin uzun yıllardır çalıştığı bir konudur. Asal sayılar, sadece kendisinden ve bir sayıdan bölünebilen sayılardır. Örneğin, 2, 3, 5, 7, 11 gibi sayılar asal sayılardır. Asal sayıların dağılımı, matematikçilerin ilgisini çeken bir konudur, çünkü asal sayılar birçok matematiksel problemin çözümünde kullanılır.
Riemann Hipotezi, asal sayıların dağılımı hakkındaki bir formül önerir. Bu formül, Riemann Zeta Fonksiyonu adı verilen bir fonksiyonla ilgilidir. Riemann Zeta Fonksiyonu, kompleks sayılar için tanımlanmış bir fonksiyondur ve asal sayıların sayısı hakkında bilgi verir. Riemann Hipotezi, bu fonksiyonun sıfırlarının konumunu belirleyerek asal sayıların dağılımı hakkında bilgi verir.
Riemann Hipotezi, asal sayıların dağılımı hakkında çok önemli bir teori olduğu için, matematikçilerin birçok problemi çözmesine yardımcı olmuştur. Örneğin, Riemann Hipotezi, birçok sayı teorisindeki problemlerin çözümünde kullanılmaktadır. Ayrıca, kriptografi gibi birçok alanda da kullanılmaktadır.
Kriptografi ve Riemann Hipotezi
Kriptografi, verilerin güvenliği için kullanılan bir teknolojidir. Bu teknoloji, mesajların şifrelenmesi ve şifreli mesajların çözülmesini sağlar. Kriptografi, birçok alanda kullanılmaktadır, örneğin bankacılık, askeri iletişim, sağlık sektörü ve hükümetler arasındaki iletişimde kullanılır.
Kriptografi, şifreleme ve şifre çözme olmak üzere iki temel işlemi içerir. Şifreleme işlemi, mesajın anlaşılmaz hale getirilmesi için kullanılır. Bu işlemde, mesaj özel bir anahtar kullanılarak şifrelenir ve sadece doğru anahtara sahip olanlar mesajı çözebilirler. Şifre çözme işlemi ise, şifrelenmiş mesajın tekrar anlaşılır hale getirilmesi için kullanılır. Bu işlemde, mesajın şifresini çözmek için doğru anahtar kullanılır.
Kriptografi, güvenli bir şekilde iletişim kurabilmek için önemlidir. Ancak, birçok kriptografi sistemi, çeşitli saldırılara karşı savunmasızdır. Bu saldırılar, mesajın şifresini çözmek için kullanılan yöntemleri ifşa ederek sistemin güvenliğini tehdit ederler.
Riemann Hipotezi, kriptografi alanında da önemli bir rol oynamaktadır. Riemann Zeta Fonksiyonu, kriptografi için kullanılan bir fonksiyondur. Bu fonksiyon, asal sayıların dağılımı hakkında bilgi verir ve şifreleme işlemi için kullanılan anahtarların güvenliği ile ilgili önemli bir rol oynar.
Riemann Hipotezi, kriptografi alanında kullanılan RSA algoritması gibi birçok şifreleme algoritmasının temelinde yatar. RSA algoritması, özellikle bankacılık ve finans sektöründe kullanılmaktadır. Bu algoritma, mesajların şifrelenmesi ve şifre çözme işlemlerinde kullanılan anahtarların oluşturulması için Riemann Zeta Fonksiyonu’nun sıfırlarının konumlarından yararlanır.
Riemann Hipotezi, matematiksel problemlerle ilgili bir hipotez olmasına rağmen, birçok alanda kullanılan pratik uygulamaları vardır. Ancak, Riemann Hipotezi, henüz kanıtlanamamıştır ve bu nedenle matematikçiler tarafından halen üzerinde çalışılmaktadır.
Sonuç olarak, Riemann Hipotezi, matematiğin en önemli açık problemlerinden biridir ve asal sayıların dağılımı hakkındaki bir teoriyi ortaya koyar. Bu hipotez, matematiksel teorilerin geliştirilmesi ve kriptografi gibi birçok alanda etkili bir şekilde kullanılmasına yardımcı olmaktadır. Eğer hipotez doğruysa, asal sayıların dağılımı hakkında daha iyi bir anlayışa sahip olunabilecek ve bu da daha güvenli şifreleme algoritmalarının geliştirilmesine yol açabilecektir. Bunun yanı sıra, Riemann Hipotezi’nin çözümü, matematiksel teorilerin genişletilmesine ve matematiğin temel prensiplerinin daha iyi anlaşılmasına da katkı sağlayacaktır.
Önerilen Yazı: Tam Açı Neden 100, 200, 300 Değil de 360 Derecedir?